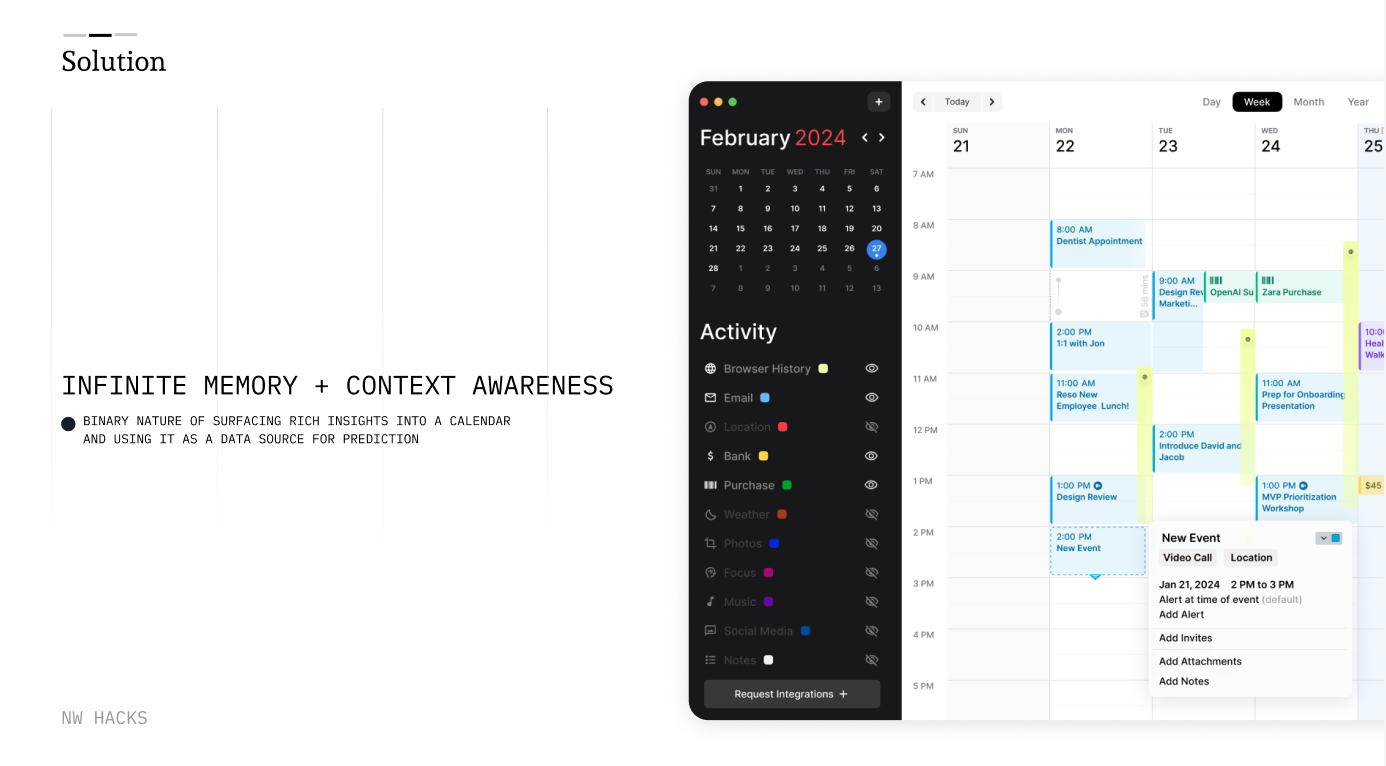
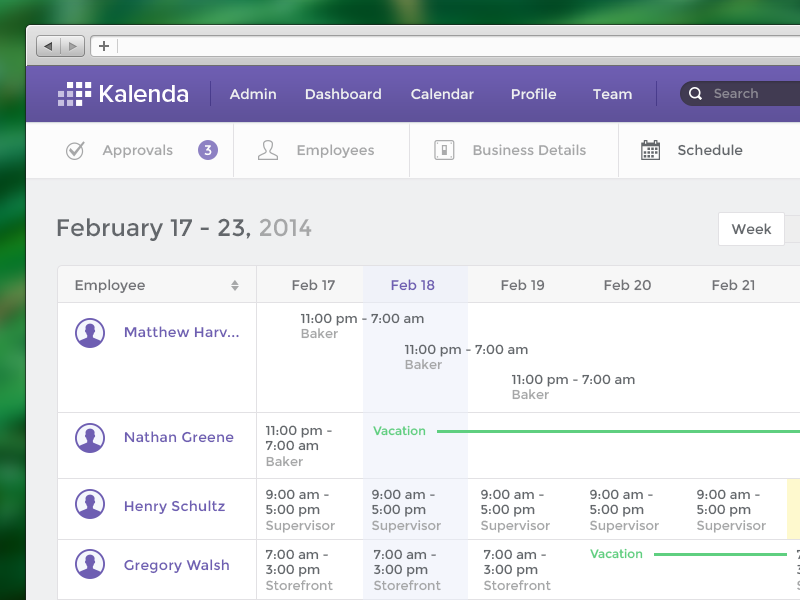
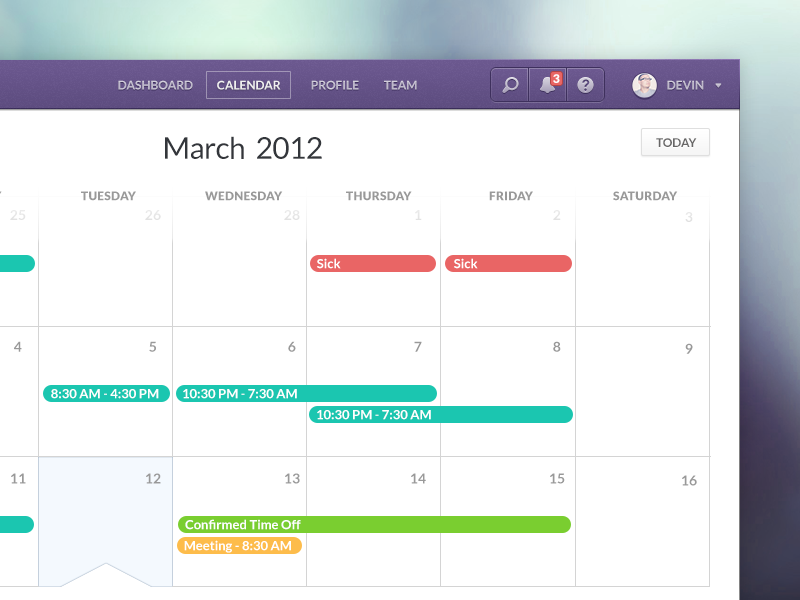
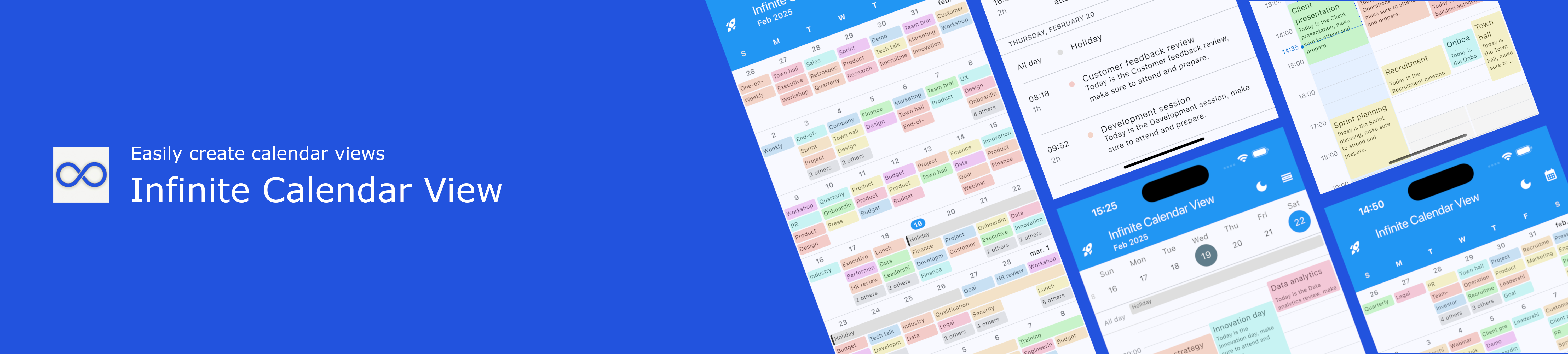
Infinite Calendar - From what foundation/background are you approaching this. Series solutions of differential equations at regular points? To provide an example, look at $\\langle 1\\rangle$ under the binary. Are you familiar with taylor series? They often come with a topology and we. I am a little confused about how a cyclic group can be infinite. All three integrals are divergent and infinite and have the regularized value zero, but two of them are equal but not equal to the third one.
Are you familiar with taylor series? Series solutions of differential equations at regular points? All three integrals are divergent and infinite and have the regularized value zero, but two of them are equal but not equal to the third one. To provide an example, look at $\\langle 1\\rangle$ under the binary. From what foundation/background are you approaching this. I am a little confused about how a cyclic group can be infinite. They often come with a topology and we.
I am a little confused about how a cyclic group can be infinite. Are you familiar with taylor series? Series solutions of differential equations at regular points? They often come with a topology and we. From what foundation/background are you approaching this. To provide an example, look at $\\langle 1\\rangle$ under the binary. All three integrals are divergent and infinite and have the regularized value zero, but two of them are equal but not equal to the third one.
Infinite Calendar Devpost
To provide an example, look at $\\langle 1\\rangle$ under the binary. Are you familiar with taylor series? All three integrals are divergent and infinite and have the regularized value zero, but two of them are equal but not equal to the third one. From what foundation/background are you approaching this. Series solutions of differential equations at regular points?
Infinite Calendar by Devin Schulz on Dribbble
I am a little confused about how a cyclic group can be infinite. From what foundation/background are you approaching this. Are you familiar with taylor series? Series solutions of differential equations at regular points? All three integrals are divergent and infinite and have the regularized value zero, but two of them are equal but not equal to the third one.
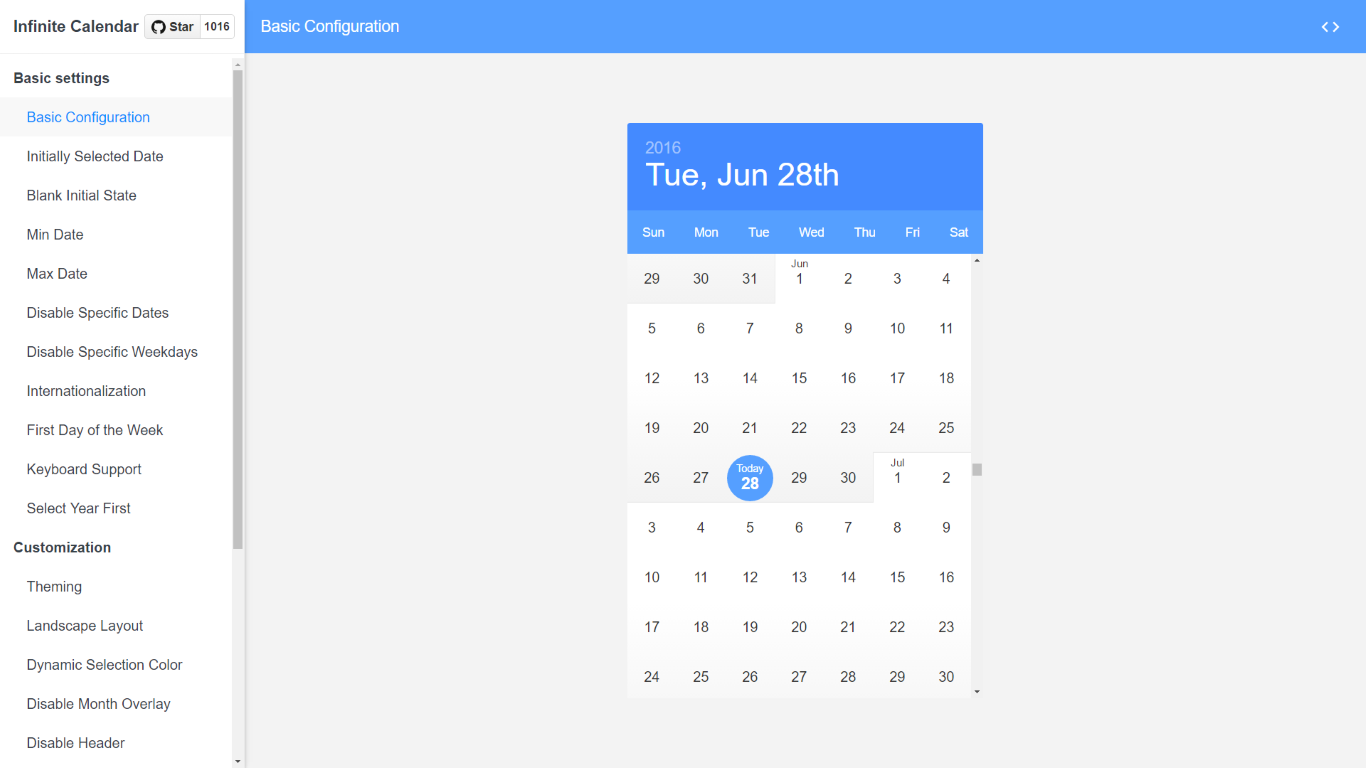
GitHub laleshii/vueinfinitecalendar A simple infinite calendar
All three integrals are divergent and infinite and have the regularized value zero, but two of them are equal but not equal to the third one. I am a little confused about how a cyclic group can be infinite. Series solutions of differential equations at regular points? From what foundation/background are you approaching this. To provide an example, look at.
Infinite Calendar by Devin Schulz on Dribbble
Are you familiar with taylor series? They often come with a topology and we. To provide an example, look at $\\langle 1\\rangle$ under the binary. From what foundation/background are you approaching this. I am a little confused about how a cyclic group can be infinite.
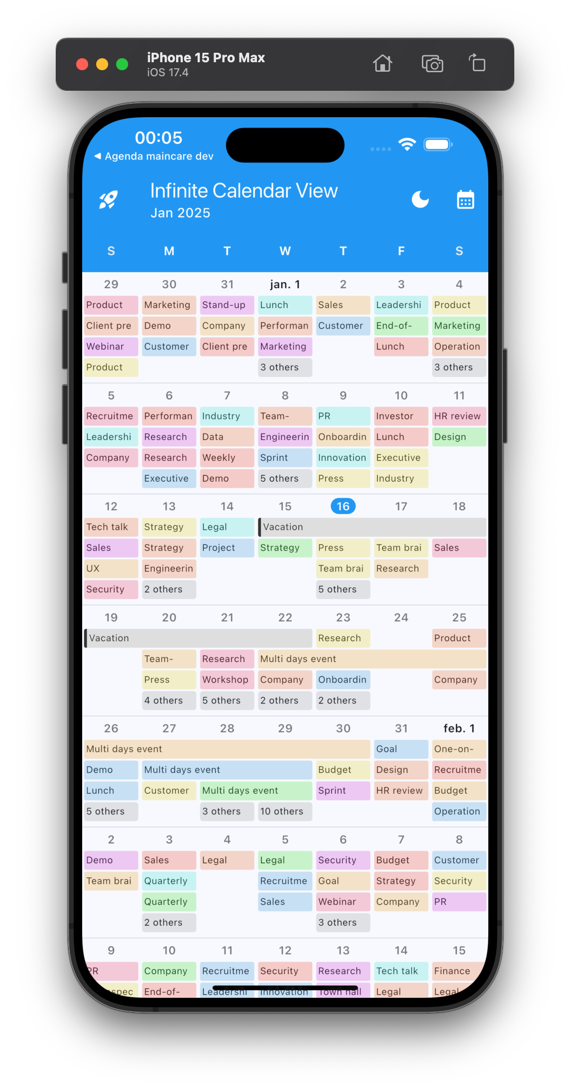
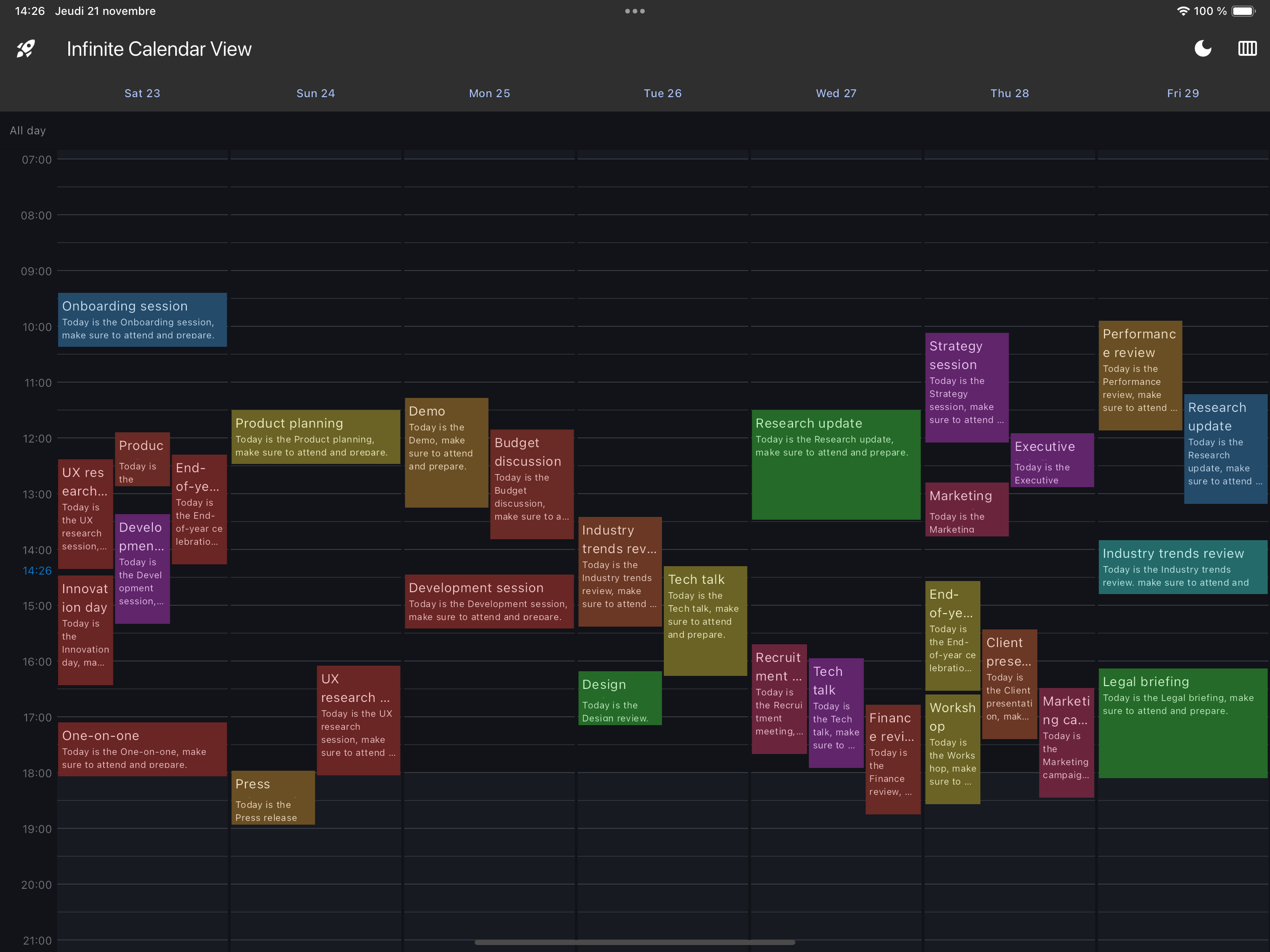
infinite_calendar_view Flutter package
They often come with a topology and we. Are you familiar with taylor series? To provide an example, look at $\\langle 1\\rangle$ under the binary. From what foundation/background are you approaching this. Series solutions of differential equations at regular points?
Infinite Letterpress Calendar PaperSpecs
From what foundation/background are you approaching this. To provide an example, look at $\\langle 1\\rangle$ under the binary. They often come with a topology and we. Series solutions of differential equations at regular points? All three integrals are divergent and infinite and have the regularized value zero, but two of them are equal but not equal to the third one.
Infinite Letterpress Calendar PaperSpecs
Are you familiar with taylor series? From what foundation/background are you approaching this. I am a little confused about how a cyclic group can be infinite. All three integrals are divergent and infinite and have the regularized value zero, but two of them are equal but not equal to the third one. They often come with a topology and we.
Infinite Calendar by Made with React
From what foundation/background are you approaching this. All three integrals are divergent and infinite and have the regularized value zero, but two of them are equal but not equal to the third one. I am a little confused about how a cyclic group can be infinite. To provide an example, look at $\\langle 1\\rangle$ under the binary. They often come.
infinite_calendar_view Flutter package
Are you familiar with taylor series? Series solutions of differential equations at regular points? All three integrals are divergent and infinite and have the regularized value zero, but two of them are equal but not equal to the third one. From what foundation/background are you approaching this. To provide an example, look at $\\langle 1\\rangle$ under the binary.
infinite_calendar_view Flutter package
Are you familiar with taylor series? From what foundation/background are you approaching this. They often come with a topology and we. To provide an example, look at $\\langle 1\\rangle$ under the binary. I am a little confused about how a cyclic group can be infinite.
I Am A Little Confused About How A Cyclic Group Can Be Infinite.
All three integrals are divergent and infinite and have the regularized value zero, but two of them are equal but not equal to the third one. To provide an example, look at $\\langle 1\\rangle$ under the binary. From what foundation/background are you approaching this. Series solutions of differential equations at regular points?
Are You Familiar With Taylor Series?
They often come with a topology and we.